
Uji Kenormalan
Kenormalan data merupakan salah satu asumsi standar pada ujiuji statistik parametrik seperti pada uji t dan uji F. Sedikit penyimpangan dari kenormalan tidaklah menyebabkan masalah yang serius. Namun penyimpangan yang jauh dari kenormalan haruslah diperhatikan. Box plot sangat membantu untuk mendapatkan informasi tentang kesimetrisan data. Selain box plot, kita juga dapat membuat histogram, diagram pencar, atau plot batang daun dari data untuk melihat penyimpangan dari kenormalan secara umum. Namun untuk itu diperlukan jumlah sampel yang cukup besar agar dapat memberikan informasi yang baik tentang bentuk distribusi dari data yang dianalisis. Cara lain untuk melihat kenormalan adalah dengan uji Lilliefors/Kolmogorov-Smirnov atau dengan uji goodness of fit. Alasan utama mengapa asumsi kenormalan data diperlukan dalam banyak situasi, karena prosedur pengujian didasari pada distribusi tyang berasal dari kenormalan.
Uji kenormalan dengan Metoda Lilliefors
Uji ini sama dengan uji kolmogorov-smirnov untuk 1 sampel, bedanya kolmogorov menggunakan varians dan rata-rata dari populasi. Lilliefors menggunakan varians dan rata-rata dari data. Hipotesanya,
Ho : data berdistribusi normal
H1 : data tidak berdistribusi normal
Dalam hal ini kita menggunakan distribusi kumulatif sampel (sample cumulative distribution) S(x) dengan probabilita kumulatif normal (normal cumulative probability) F(x). Jika Ho benar maka S(x) harus serupa (similar) dengan F(x). S(x) didefinisikan sebagai proporsi dari nilai sampel yang lebih kecil atau sama dengan x. Statistik ujinya adalah statistik uji D.
Keputusan : Tolak Ho jika D > nilai tabel liliefors
Contoh:
Sampel random independen dari 6 asisten profesor. Mereka ditanya untuk memperkirakan jumlah waktu di luar kelas untuk menghabiskan tanggung jawab mengajar pada minggu lalu hasilnya dalam jam, ditunjukkan pada data di bawah ini: (gunakan α = 5 %)
Asisten: 7, 12, 11, 15, 9, 14.
Solusi:
Ho : data berdistribusi normal
H1 : data tidak berdistribusi normal
Berdasarkan data diatas didapat rata-rata dan standar deviasi seperti berikut:
D = 0.1127
Dtabel, (tabel lillifors) pada n = 6 dan α = 0,05 adalah sebesar 0.319
Keputusan : Terima Ho, karena nilai D< Dtabel
Kesimpulan : data asisten berdistribusi normal dengan tingkat keyakinan sebesar 95%.
Uji kenormalan dengan goodness of fit test
Pada uji ini data dibagi dalam beberapa interval, kemudian dihitung probabilita masing-masing interval. Probabilita dihitung dengan menggunakan distribusi normal dengan rata-rata ( ) dan standar deviasi (S) sebagai estimator dari μ dan σ .
) dan standar deviasi (S) sebagai estimator dari μ dan σ .
 ) dan standar deviasi (S) sebagai estimator dari μ dan σ .
) dan standar deviasi (S) sebagai estimator dari μ dan σ .
Hipotesa:
H0 : data berdistribusi normal
H1 : data tidak berdistribusi normal
α adalah tingkat keberartian ; k = banyaknya interval
Oi adalah jumlah observasi pada interval ke-i
Ei adalah jumlah harapan pada interval ke-i
Ei = n . Pi
n adalah jumlah observasi
Pi adalah probabilita observasi pada interval ke-i yang dihitung dengan menggunakan distribusi normal.
Keputusan:
Contoh:
Rata-rata modal 10 perusahaan PMA adalah sebagai berikut (dalam juta US$):
56 58 60 64 54 52 50 40 47 60
Ujilah apakah data tersebut berdistribusi normal dengan α = 5%?
Solusi:
Data dibagi dalam beberapa interval, dalam hal ini dibagi menjadi 4 interval (jumlah interval biasanya disesuaikan dengan banyaknya observasi)
Nilai harapan tiap interval:
E1 = n . P1 = 10 . 0,1587 = 1,587
E2 = n . P2 = 10 . 0,3413 = 3,413
E3 = n . P3 = 10 . 0,3413 = 3,413
E4 = n . P4 = 10 . 0,1587 = 1,587
Jumlah observasi tiap interval:
O1 = 1 ; O2 = 4 ; O3 = 4 ; O4 = 1 .

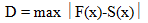



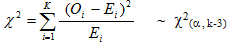



Post a Comment